[[[[# DT Gedächtnisprotokoll Wise 2020/2021 *Ein kollaborativ erstelltes Gedächtnisprotokoll für die DT Klausur im WiSe 2020/2021.* ## Aufgabe 1: Informationsmengen, Zahlensysteme und Zahlendarstellungen ### 1.1 1. Geben Sie *zwei* Arten der Bitlängenerweiterung (?) an: > 1. zero-padding (unsigniert) (-> war es nicht zero-extension in der Vl?) > 2. sign-extension (beim Zweierkomplement) 3. Warum kann man ein Nibble direkt in das Hexadezimalsystem übersetzen? > Mit einem Nibble kann man 2^4 = 16 Zustände darstellen, dies entspricht der Basis des Hexadezimalsystems. 5. Wieso ist die Zahl $-1$ in Zweierkomplement immer mit voll gesetzten 1-en unabhängig von der Bitlänge > Weil das MSB gleich 1 sein muss und das Zweierkomplement per sign-extension erweitert wird, und dadurch alles mit 1en aufgefüllt wird. ### 1.2 Tabelle mit min und max Werten von zwei Zahlen für u, bv und zk. (Übung 1.3.1) | $k$ | vorzeichenlos u |]]]](https://)(https://)(https://)(https://) Betrag-Vorzeichen | Zweierkomplement | | ---- | --------------- | ------------------------------------ | --------------------------- | | $3$ | 0; $2^3-1 = 7$ | $-(2^{3-1}-1) = -3$; $2^{3-1}-1 = 3$ | $-2^2 = -4$; $2^2 -1 = 3$ | | $5$ | 0; $2^5-1 = 31$ | $-(2^4 - 1) = -15$; $2^4 -1 = 15$ | $-2^4 = -16$; $2^4 -1 = 15$ | ### 1.3 Sowas wie $13_7 - 11_6$ (gerne aktualisieren, falls es genauere Zahlen oder einen besseren Rechenweg gibt) 1. Beide Zahlen als Zweierkomplement aufschreiben, 1 Byte Länge. $$ \begin{align} 13_7 = 1 \cdot 7^1 + 3 \cdot 7^0 = 7 + 3 = 10_{10} = 0000 1010_2 \\ 11_6 = 1 \cdot 6^1 + 1 \cdot 6^0 = 6 + 1 = 7_{10} = 0000 0111_2 \end{align} $$ 3. Zweiten Summanden negieren $$ \overline{00000111_2} + 1 = 11111000_2 + 1 = 11111001_2 $$ 6. Addieren. $$ \begin{align} 00001010_2\\ \underline{11111001_2} \\ 00000011_2 \end{align} $$ 7. Das Ergebnis in Dezimalzahl umrechnen. $$ \begin{align} 00000011_2 = 3_{10}\\ \end{align} $$ ## Aufgabe 2: Wahrheitstabellen und Physikalische Realisierung von Logikgattern ### 2.1 a) Parität von $m$ Wörtern mit $n$ Bit-Breite. Wie viele (Parität-)Bits werden insgesamt benöntigt (für Längen und Breitenparität) >m*(n+1) b) Erklären Sie die abstrakte Funktionsweise eines Transistors >Transistoren sind spannungsgesteuerte Schalter mit zwei Anschlüssen(Source und Drain) die durch einen dritten Eingang(Gate) je nach Spannung verbunden oder getrennt sind. c) Erklären Sie die Funktionsweise eines MUX (oder so ähnlich). >Ein Multiplexer hat $A_0$ bis $A_n$ Eingänge und ein Ausgangssignal Y. Mit Hilfe des Steuersignals S wird eine der Eingänge ausgewählt und an den Ausgang Y weitergeleitet. d) Erklären Sie die Funktionsweise eines Decoders (oder so ähnlich). >Ein Decoder hat $n$ Eingänge und $2^n$ Ausgänge. Je nach Belegung der Eingangssignale wird genau einer der Ausgänge auf 1 geschaltet. ("One-Hot Kodierung") ### 2.2 Funktion $Y = \overline{(AB) + C}$ in CMOS Struktur implementieren, wobei das Pull-Up Netz in Form eines Pseudo-nMos dargestellt werden soll. ### 2.3 Glaube hier war Wahrheitswertetabelle ausfüllen: iwie ($Y = (\overline{\overline{A}B) + ((A+\overline{B}) \ \oplus \ AC)}$) <!-- Idee: Vereinfachen: $(A+\overline{B}) \overline{A(\overline{B}\overline{A} + AB)C)}$... oder Zwischenergebnisse --> | $A$ | $B$ | $Y$ | | --- | --- | --- | | $0$ | $0$ | $0$ | | $0$ | $1$ | $0$ | ## Aufgabe 3: Kombinatorische Logik, Boole’sche Algebra und Karnaugh Diagramme ### 3.1 1. Zwei Eigenschaften kombinatorischer Logik >Pfade sind zyklenfrei > >Verbindunsknoten sind entweder Schaltungseingänge oder an Treiber eines Schaltungselements angeschlossen 3. Beschreiben Sie die Begriffe Maxterm und DNF > Ein Maxterm ist die Summe über alle Eingangsvariablen . > DNF ist die Disjunktive Normalenform bzw. die Summe aller Minterme(Produkt über alle Eingangsvariablen) für die die Funktion wahr wird. 5. Erklärung bezüglich des Axioms A1/A1' 6. Erklären Sie was "Grey Code" ist > Grey-Code ist ein Binär-Code, bei dem Nachfolger sich nur um 1 bit von dem aktuellen Wert unterscheiden. Bspw. $1_{10} = 001_{grey}, 2_{10} = 011_{grey}$. Der Vorteil ist, dass nur jeweils 1 bit geflippt werden muss, wenn hoch oder runter gezählt wird. 8. Und wie Grey-Code bei Karnaugh-Diagrammen eingesetzt wird ### 3.2 T7 $(AB)C = A(BC) = Y$ mit Wahrheitstabelle beweisen (leere Zellen ausfüllen) | A | B | C | AB | BC | Y | | - | - | - | -- | -- | - | | 0 | 0 | 0 | 0 | 0 | 0 | | 1 | 1 | 0 | 1 | 0 | 0 | | 0 | 1 | 1 | 0 | 1 | 0 | | 1 | 1 | 1 | 1 | 1 | 1 | ### 3.3 Pull Down von einem Term ($Y = \overline{\overline{A}B + A\overline{B}}$ auf jedenfall war der komplette Term negiert) mit Pseudo-nMos-pull-up. Funktion $Y = (\overline {(\overline {A} + B) (A+ \overline {B})}$ erst mit bool'schen Regeln vereinfachen und dann nur mit 2Input XOR Gattern darstellen. ## Aufgabe 4: Logikminimierung und -realisierung ### 4.1 1. Nennen Sie vier Arten wie man Logik minimiert > >1. KV-Diagramme >2. Bubblepushing >3. Espresso (Zählt das wirklich? müsste eigentlich) >4. per Boolesche Axiome vereinfachen > 2. Erklären Sie *Maxterm* und *DNF*: Maxterm: > Summe/Oder-Verknüpfung (Disjunktion) zwischen allen Eingangsliteralen. >DNF: > Disjunktive Normal-Form oder auch Sum-of-products. Alle (Min-)Terme, welche gleich Eins sind. 3. Boolesche Dualität erklären ### 4.2 #### Espresso Espresso lesen und ich glaube Terme rausschreiben. ``` .i 3 .o 1 .il A B C .p 4? 01- 1 1-0 1 101 1 --1 1 .e ``` $Y = \overline{A}B + A\overline{C} + A\overline{B}C + C$ (in dem anderen Gedächnisprotokoll stand dass wenn da .ilb A B C steht, dann muss es von rechts nach links gelesen, ist richtig?) #### NOR-Gates Mit nur NOR-Gates folgenden Term darstellen: $Y = \overline{\overline{A}B + A\overline{B}}$ Zuerst Term mit booleschen Axiomen/Theoremen komplett zu NOR-Gates umwandeln: Äußerer ist schon ein NOR. Inverter/Not: $\overline{A} = \overline{A + A}$ And: $AB = \overline{\overline{AB}} = \overline{\overline{A} + \overline{B}}$ $$ Y = \overline{\overline{A + \overline{B}} + \overline{\overline{A} + B}} $$ Alternative Darstellung: ``` NOR( NOR( A NOR(B B) ) NOR( NOR(A A) B ) ) ``` ### 4.3 ## Aufgabe 5: Speicherelemente ### 5.1 a) Beschreiben Sie die bistabile Grundschaltung. >Bistabile Grundschaltung ist die Grundlage des Zustandsspeichers. Sie besteht aus >2 Invertern mit Rückkopplung und speichert 1 Bit durch stabile Zustände. >Jedoch kann nicht Beeinflusst werden, welcher Zustand gespeichert wird b) Was bedeutet es wenn Speicherelemente Taktphasen gesteuert sind? >Sie sind die Hälfte der Zeit transparent > b.2) Nennen Sie ein Taktphasen gesteuertes Speicherelement. > > D-Latch ist Taktphasen gesteuert > c) Nennen Sie zwei Verwendungsmöglichkeiten von Speicherelementen mit Taktfreigabe. >Zähler, Speicher mit Adressdecoder ### 5.2 D-Latch entwerfen mit einem *asynchronen* Reset ($RST$) und nur **einem weiteren** Gatter, einem SR-Latch (Set-Reset), Input $D$, $CLK$ und Outputs $Q$ und $\overline{Q}$. ### 5.3 Timinganalyse (vgl. Ü6.2.1 WiSe 20/21) und ankreuzen Tabelle ob D-Latch oder D-FF. #### Mehrwertige Logik Gegeben: Kleine Zeichnung mit Gattern. X und Z treten auch auf. Wahrheitstabelle fertig ausfüllen. ## Aufgabe 6: Zeitverhalten synchroner sequentieller Logik und Parallelität ### 6.1 1. Fragen zu Taktphase + Beispiel 2. Frage zu Taktflanke 3. Fragen zu $t_\text{skew}$ (wie ist das definiert) >$t_\text{skew}$ bezeichnet die maximale Differenz der Taktankuftszeit zwischen zwei Registern > 5. Was ist die "Verbotene Zone"? 6. Wann sollte man möglichst viele Pipelinestufen verwenden? > Wenn man eine geringe Latenz braucht, da viele Pipelinestufen zu einer hohen Latenz führen ### 6.2: #### Impfzentrum Parallelität Tabelle ausfüllen mit unterschiedlichen Zeiten (zwei Ärzte, zwei Artzhelfer) (nicht ein Arzt? bin mir ziemlich sicher war ein Artz 2 Helfer) Drei Schritte: 1. Desinfizieren 1min, 2. Impfen 1min, 3. Eintragung im Impfpass 1min - Artzhelfer kann Desinfizieren & Eintragen im Impfpass - Arzt kann Impfen & Eintragen im Impfass Sequentiell, räumlich parallel, zeitlich parallel, Pipelining. Zu zeigen war der Durchsatz (min/pro Person) und die Latenz (Personen/Stunde) #### Timing Diagram D-Latch und FF im Timing Diagramm (mit $D_n$ und $Q_n$) erkennen. (schienen auch etwas zeitversetzt zu sein) | $n$ | D-Latch | FF | | --- | ------- | -- | | $1$ | x | | | $2$ | | x | | $3$ | | x | | $4$ | x | | | $5$ | | x | | $6$ | x | | ### 6.3 Diagram und Timings aufgelistet. 1. Berechnen von $t_\text{cd}$ > $= t_\text{cd,XOR} = 30ns?$ 3. $t_\text{pd}$ der kombinatorischen Schaltung (min und max, der Pfad war angegeben) > $= t_\text{pd,AND} + t_\text{pd,OR} + t_\text{pd,XOR} = 80ns + 80ns + 60ns$ 5. Frequenz berechen > $\dfrac{1}{t_\text{pcq} + t_\text{pd} + t_\text{setup}} = 90ns + 220ns + 90ns = 400ns = 0,4\mu s$ > und 1/400ns = 0,0025 in GHZ umwandeln = 2,5GHZ? 7. Timing überprüfen: > $t_\text{ccq} + t_\text{cd} \ge t_\text{hold} \iff 50ns + 30ns = 80ns \ge 50ns$ (das war wahr, also nichts verletzt) ## Aufgabe 7: Endliche Automaten ### 7.1 1. Warum braucht man kombinatorische Logik zur Automatendarstellung? >Kombinatorische Logik wird für die Realisierung der Schaltung des Automaten benötigt 2. Nenne zwei Arten, wie Automaten dargestellt werden können. > Mealy- & Moore Automaten 3. Warum kann die FSM Dekomposition hilfreich sein? > FSM Dekomposition = Aufteilen **komplexer** FSMs in **einfachere** interagierende FSMs > Also: Komplexes Problem einfacher darstellen ### 7.2 Karnaugh: 1. Primimplikanten <p><a href="https://instant-famous.com/de/collections/tiktok-aufrufe-kaufen" target="_blank">markieren</a></p> 2. Minterme für $S_0'$ und $S_1'$ ablesen. 3. Gatter-Zeichnung vervollständigen (Zwei FF für S waren gegen, wo beide Ausgänge zu $Y$ gingen und die Eingänge $S_0'$ und $S_1'$ waren. Davor sollte gezeichnet werden, also die Minterme eingetragen werden.) ### 7.3 Moore-Automat (drei Zustände) in Verilog zu Mealy mit einem Zustand weniger umschreiben. - $S_0 \xrightarrow{a} S_0$ - $S_0 \xrightarrow{\overline{a}} S_1$ - $S_1 \xrightarrow{a} S_2$ - $S_1 \xrightarrow{\overline{a}} S_1$ - $S_2 \xrightarrow{a} S_2$ (oder zu $S_0$) - $S_2 \xrightarrow{\overline{a}} S_1$ - $Y = S_2$ ```verilog= module moore(input logic [2:0] S, input logic A, output logic Y) typedef enum logic [2:0] {S0, S1, S2} statetype; statetype state, nextstate; // TODO: Gab es CLK und RST? always_ff @(posedge CLK) state <= RST ? S0 : nextstate; // TODO: Logik anpassen always_comb case(state) 0: nextstate = A ? S0 : S1; 1: nextstate = ~A ? S1 : S2; default: nextstate = A ? S0 : S1; // 2: nextstate = A ? S0 : S1; // default: nextstate = S0; endcase assign Y = (state == S2); endmodule ``` Lösungsidee: ```verilog= module mealy(...) typedef enum logic [1:0] {S0, S1} statetype; ... assign nextstate = A ? S0 : S1; assign Y = (state == S1) && (~A); endmodule ``` ## Aufgabe 8: Arithmetische Grundschaltungen ### 8.1 ### 8.2 1. Stelle die Rechnung `((x+x)*1024) / 8` mit nur einer Shiftoperation dar. x<<<8 oder x<<8 = 2^8 = 2\*1024/8 x<<<1 x<<<10 x>>>3 Stimmt das? $$\begin{align} ((x + x) \cdot 1024) / 8 \\ (2x \cdot 1024) / 8 \\ (2^1x \cdot 2^{10} ) / 2^3 \\ 2^{11}x / 2^3 \\ \frac{2^{11}}{2^3} x \\ x \cdot 2^{11 - 3}\\ x \cdot 2^{8} \end{align}$$ Es gilt $n$ Shifts von $x$ ist $x \cdot 2^n$, also shiften wir $8$ mal nach links: `x << 8`. (Hier ist auch egal, ob es ein arithmetischer oder logischer Shift ist, da beide mit $0$ auffüllen.) ### 8.3 Berechnung von 4 (oder 6?) XORs und 2 (oder 3?) ORs **strukturell** in Verilog umsetzen, also keine Operatoren wie `==, >=, ...` verwenden. Gegeben waren `xorGate(A,B,Y)` und `orGate(A,B,Y)`. Lösungsidee: ```verilog= module calc(input logic [3:0] A, B, output logic Y); logic x1, x2, x3, x4, o1, o2; xorGate xor1(.A(A[0]), .B(B[0]), .Y(x1)); xorGate xor2(.A(A[1]), .B(B[1]), .Y(x2)); xorGate xor3(.A(A[2]), .B(B[2]), .Y(x3)); xorGate xor4(.A(A[3]), .B(B[3]), .Y(x4)); // alternative Schreibweise orGate or1(.A(x1), .B(x2), .Y(o1)); orGate or2(.A(x3), .B(x4), .Y(o2)); orGate or3(.A(o1), .B(o2), .Y(Y)); endmodule ``` ## Aufgabe 9: SystemVerilog ### 9.1 1. Wofür ist die Synthese bei System Verilog > Um den Code in Hardware zu beschreiben und zu sehen, wie viele Elemente benötigt werden. 2. Wofür ist die Simulation von System Verilog > Gut zum Testen vor allem vom Timings und zum Finden und Eliminieren von Glitches. 3. Nenne ein Element welches simulierbar, aber nicht synthetisierbar ist. > Delay `#(time)` 3.1. Nennen die Funktionsweise dieses Elements ### 9.2 Gegeben sei eine Vorzeichenbehaftete Bitfolge der Größe k. Bitfolge soll mit nur Kombinatorischen Ausdrücken in Zweierkomplement überführt und ausgegeben werden > //assign Y = (~a) + 1; Stimmt nicht, da 1011 (-3) so zu 0100+1=0101 (+5) konvertiert wird > assign Y = A[k-1] ? {1'd1, ~A[k-2:0] + 1} : A; (Falls das erste Bit eine 1 ist, den Rest negieren und 1 addieren; sonst Zahl belassen) ### 9.3 Test-Suite für `module addr(input logic [2:0] A, B, output logic [3:2] Y);` schreiben. Vorgegeben war der groben *module* Rahmen mit den zwei Bereichen. - Rechnung : `assign S = A + B` - 1. Wires für Rechnung in Verilog schreiben - 2. Ausschöpfende Tests schreiben - 3. wenn Rechnung falsch -> "Falsch!" ausgeben Test auf Ungleicheit: Bits auf unterster Stufe mit XOR Gattern, danach OR-Baum => Umsetzung in System Verilog: Gegebene Sub-Module XOR-Gate und OR-Gate und Implementation mit generate Block für `input logic [3:0] A, B` ## Aufgabe 10: Speicher- und Logikfelder ### 10.1 1. Wie werden die DRAM Speicherelemente in der Hardware realisiert? > Durch Kondensatoren 3. warum muss DRAM häufiger aktualisiert werden > Die Speicherelemente verlieren durch Leckstrom mit Zeit ihre Bits. 5. Warum muss DRAM nach dem Lesen neu geschrieben werden? > Weil die Kondensatoren dabei entladen werden. 7. Was bedeutet ASIC? > Anwendungsspezifischer integrierter Chip/Schaltkreis (application-specific integrated circuit) 8. Was ist FPGA? Was ist der Unterschied zu ASIC > FPGA (Field Programmable Gate Array) vereint Flexibilität von Software-Prozessoren ("im Feld programmierbar") mit Performanz von ASICs (optimierte "Basisgatter-Schaltungen") 9. Was bedeutet PLA? > Programmable Logic Array - Realisiert einfache komb. Logik via *Sum-of-Products* (DNF) 11. Was ist der Unterschied zu PAL? 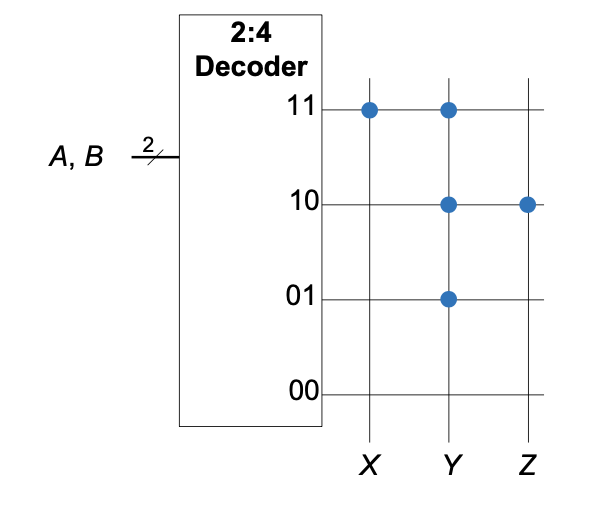> Programmable Array Logic (PAL): nur Eingabefeld programmierbar > Bei PLA im Unterschied zu PAL sind sowohl Eingabefeld als auch Ausgabefeld programmierbar ### 10.2 #### ROM wordline, bitline mit Punkten: $X, Y, Z$ aus Punkt-Matrix bestimmen. 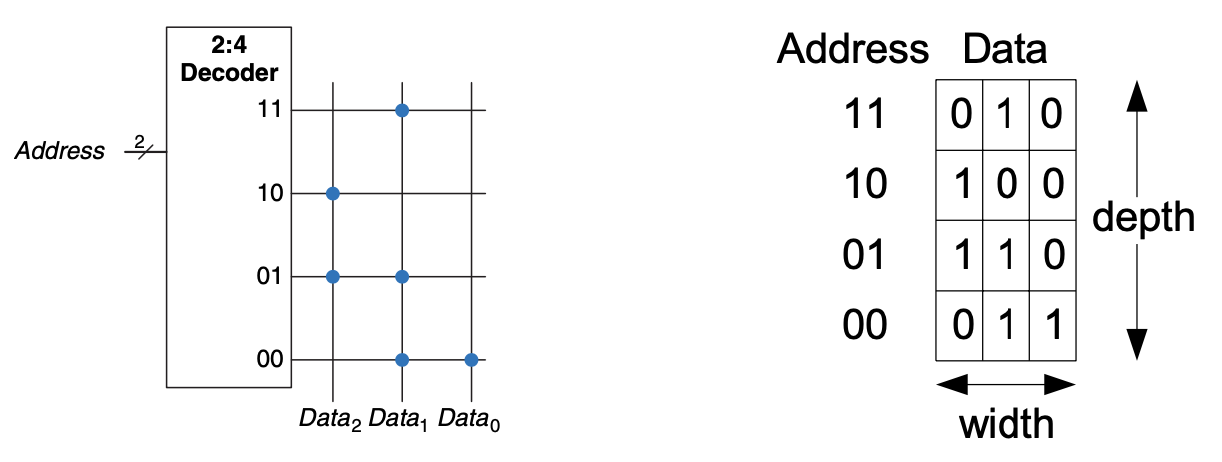(VL11 , Folien 26-29 WiSe 20/21)  #### RAM wordline, bitline mit Punkten: $X, Y, Z$ aus bestimmen. (VL11 , Folien 26-29 WiSe 20/21)  ### 10.3 Implementieren Sie einen Barrel-Shifter (glaube ein anderer)? mit nur zwei MUX4 und drei MUX2 und einem Gate. (müsste ähnlich zu dem Shifter-Beispiel aus der Vorlesung sein)